반응형



사람들이 실생활에서 삼각함수를 활용할 수 있다고 하는걸 주변 동료에게 들었습니다. 그래서 그게 무슨말이냐고 했더니, 자기도 정확한건 모르는데 TV에서 일반인이 나와서 삼각함수를 일상생활에 적용하는걸 본적이 있다고 하더군요. 궁금한건 못참는 성격이라 또 한번 찾아봤습니다.



삼각함수란?
삼각함수 실생활 활용법을 알아보기 전 먼저 삼각함수가 무엇인지에 대해서 알아 볼게요. 직각 삼각형이 있으면 각도와 변이 있죠. 그것을 함수로 표현한거라고 생각하면 쉬운데요, 대표적으로는 사인, 코사인, 탄젠트 이렇게 나눠지고 있습니다.


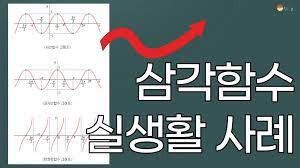
좌표평면 위 원 내에서 얻을 수 있는 선분들의 길이로 정의할 수 있는 요소입니다. 좌표를 그려놓고 평면 위 원에서 얻을 수 있는 선분의 길이를 체크해두면 직각 삼각형 각도와 변 길이와 사묻 다른 것을 볼 수 있는데요,



이 좌표 위에서 표시를 하게 되면 무한급수와 그래프로 표현할 수 있습니다. 위 아래로 s자 모양을 그리고 있는 모습이며 마치 파도를 보는 것 같은데요, 주기적으로 나타나는 현상들을 그래프로 표현이 가능하다는 뜻이기도 합니다.



삼각함수의 유래
우리의 생활속에서 살펴 보면 삼각함수 실생활 활용법으로는 소리와 전파, 빛 등이 있습니다. 주기적으로 나타나는 현상들이죠. 특히 피타고라스라는 수학자이자 철학자는 음악 속에 수학이 존재한다는것을 처음 발견하기도 했는데요, 대장장이의 망치질 소리를 듣고 음을 느낄 수 있었고 망치의 크기에 따라서 음이 달라진다는 것을 발견할 수 있었습니다.



그래서 대장간으로 가서 이것 저것 확인을 해 보며 깨달았다고 합니다. 단순히 귀로 들리는 것처럼 느껴질 수 있지만 소리는 파동이라는 것을 타고 합성되는 방식인데요, 그러니 이런 현상들을 삼각함수로 정리해둘 수 있다는 것이죠.



파형 자체를 분석하는것만으로도 어떤 악기에서 낸 소린지 알 수 있게 되는 것입니다. 그 외에도 잔잔한 물에 돌을 던져 보았을 때 나타나는 파동, 공명 현상으로 인해 무너지는 다리 등의 사례들을 확인할 수 있습니다. 국내뿐만 아니라 해외에도 다양한 사례가 있는 만큼 우리에게도 밀접하게 연결되어 있다는 뜻이기도 하죠.



이렇게 일시적인 현상 속에서도 삼각함수 실생활 활용법을 찾아볼 수 있지만 지속적인 사인 곡선도 있습니다. 국내 서해안만 보아도 알 수 있는데요, 조수 간만의 차가 크기 때문에 해수면의 높이가 달라지게 되고 그 안에서 sin곡선이 발견되곤 합니다.
라디오
해수면의 평균 높이에서 위로 올라가면 만조가 되고 낮아지면 간조가 되는 것인데 이가 반복되면서 이러한 모양이 생기는 것입니다. 우리의 생활 속에서 가장 근접하게 볼 수 있는 것은 바로 라디오이죠.



주파수를 맞춰서 소리를 들리도록 하는 방식인데요, 이 외에도 악기를 조율한다거나 비가 올 때 바람의 세기를 알아볼 때, 비가 내리는 각도를 체크할 때 모두 수학의 원리를 이용해서 완성이 되는 것입니다. 단순히 수를 잘 안다고 해서 이러한 공식이 완성되는 것은 아닙니다. 이 외에도 삼각함수 실생활 활용법은 다양하기 때문에 바이오리듬이나 노이즈캔슬링 등과 같은 요소들을 체크하면서 알아보는 게 좋습니다.
반응형